Before examining Analysis of Variance (ANOVA), it is critical to have firm a understanding of hypothesis tests and the logic underlying them. To review hypothesis tests, I am turning to Anderson et al. (2018).

Hypothesis Tests

Hypothesis tests are tentative assumptions about a population parameter and can be conducted about a population mean or proportion. The difficulty with hypothesis testing is that “it is not always obvious how the null and alternative hypotheses should be formulated” (Anderson et al., 2018, p. 389). As such, the researcher or individual reviewing a study, must consider how the hypotheses should be and are stated, as well as the context of the situation that they are formed in. In other words, a hypothesis should be structured in a way that provides the information the researcher wants to get at.

Two questions to ask when formulating hypotheses, as recommended by Anderson et al. (2018):

1. “What is the purpose of collecting the sample?” (p. 389)
2. “What conclusions are we hoping to make?” (p. 389)

When conducting research, hypotheses should be formed before selecting a sample to avoid bias. In addition, the alternative hypothesis is often created first as it reflects the conclusions the researcher hopes to support.

After hypotheses have been stated, the criteria for a decision must be set. This means that the level of significance or alpha level is decided before a test is run. In other words, what sample means are likely or very unlikely to be obtained if the null hypothesis is true. It is common to us .05, .01, or .001 as the alpha levels.

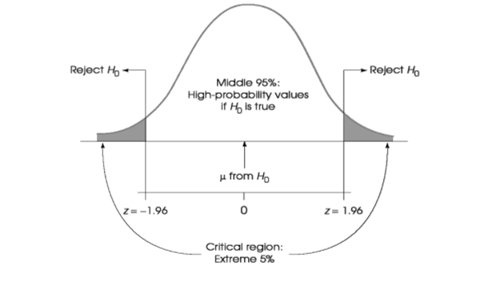
It is the extremely unlikely values that make up the critical region or where the null hypothesis is rejected. The critical region is defined by the alpha level.

Once a level of significance is decided on, then data can be collected, and sample statistics run. The final step is to make a decision: reject or fail to reject the null hypothesis.

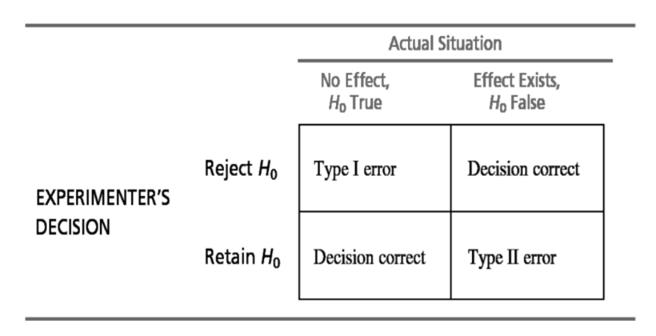
As hypothesis tests are conducted using limited information from a sample, there is always the chance that the sample is misleading. If a sample is not representative of the population, two kinds of errors can be made: type I errors or type II errors.

Additional information: https://opentextbc.ca/introstatopenstax/chapter/null-and-alternative-hypotheses/

Analysis of Variance

Analysis of variance, or ANOVA, is used to compare the mean differences of two or more treatments. Basically, ANOVA evaluates the total amount of variation in the dataset by looking at variation as the amount that can be ascribed to chance and the amount ascribed to the treatment effect.

• Between-groups variance: measures the differences between sample means (variance is due to chance and treatment effect – some variance is expected)
• Within-groups variance: measures variability within each sample (variance is due to chance alone)

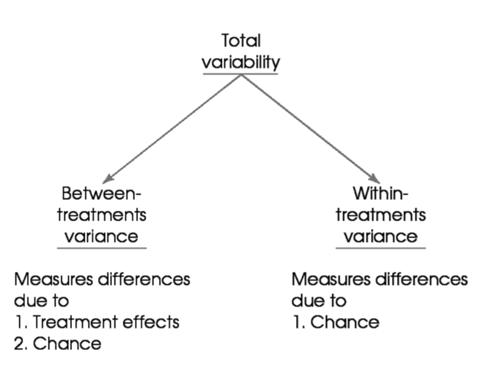
Overall, ANOVA is when between- and within-treatments variance are compared. If they are very similar, the null hypothesis cannot be rejected (i.e., the F value is close to 1). However, if there is a large difference, there is a treatment effect so reject the null hypothesis (i.e., the F value is much larger than 1).

A final note on ANOVA – a significant F ratio is not enough to make a causal inference. If the data were not obtained from a well controlled experimental design, alternative hypotheses are difficult to rule out making causal inferences inappropriate.

Additional information:

• Review of one-way ANOVA: https://opentextbc.ca/introstatopenstax/chapter/introduction-25/
• One-way ANOVA lectures: https://edge.sagepub.com/field5e/chapter-specific-resources/12-glm-1-comparing-several-independent-means/oditis-lantern
• The lab for this section has an excellent review of the main concepts of ANOVA and multiple comparison procedures

Multiple Comparison Procedures

ANOVA can tell us that not all means are equal, but it does not tell us which mean differences are responsible for a significant F value. To determine where the difference occurs, analysis of multiple comparisons must be used.

Each comparison is basically its own hypothesis test. They can be planned or unplanned (used mainly for exploratory research), as well as pairwise or complex. After deciding on the type of comparison or comparisons that are needed, the next step in multiple comparison procedures is to assign weight coefficients, similar to dummy coding, to indicate which group means are being compared.

For the tests themselves, I am not going to outline them here, but additional information on what comparisons are possible and how to decide what comparison method to use can be found below:

• Using multiple comparisons: https://support.minitab.com/en-us/minitab/18/help-and-how-to/modeling-statistics/anova/supporting-topics/multiple-comparisons/using-multiple-comparisons-to-assess-differences-in-means/
• Decision tree for multiple comparison method: https://www.statsdirect.com/help/analysis_of_variance/multiple_comparisons.htm
• Comparison methods: https://stats.libretexts.org/Bookshelves/Applied_Statistics/Book%3A_Natural_Resources_Biometrics_(Kiernan)/05%3A_One-Way_Analysis_of_Variance/5.02%3A_Multiple_Comparisons
• An overview of multiple comparisons

Final Thoughts

When completing the course work on ANOVA and multiple comparisons, I found the topics very straightforward. However, part of the reason for thinking these topics were perhaps simpler is due to the fact that I did not have to consider which methods to use. I believe if I ever need to do my own research that requires multiple comparisons, this will be an area where I will need to rely heavily on a quantitative expert’s advice for what is best and why. In other words, I may have established some foundational knowledge and skills in statistics, but I am far from ready when it comes to designing a quantitative study and deciding what tests need to be run and why.

References

Anderson, D. R., Sweeney, D. J., Williams, T. A., Camm, J D., & Cochran, J. J. (2018). Statistics for Business & Economics (13th ed., revised). Cengage Learning.