The final two topics covered in this course were within-subjects designs and mixed designs. As I mentioned in my last post, many of the topics in this course have built on preceding ones. So, I would like to pause and remind myself of the variety of ANOVA tests that are possible:
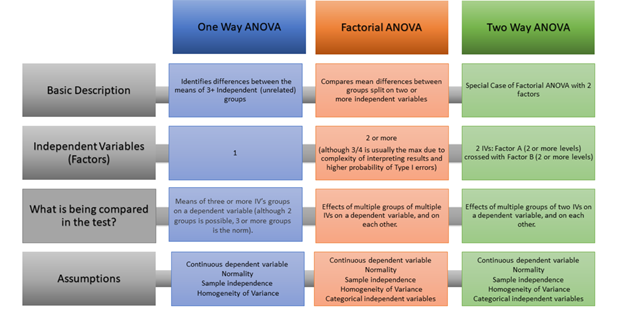
This ANOVA comparison table provided by Stephanie Glen (https://www.datasciencecentral.com/profiles/blogs/one-way-vs-two-way-anova-factorial-anova-a-comparison-in-one-pict) is a reminder of the subtle differences between the ANOVA tests and the importance of knowing which one to select. This decision is made based on the variables and the questions being asked.
We can now turn to within-subjects designs and mixed designs, where the designs’ assumptions and limitations can play a major role in their usefulness.
Within-subjects Designs
[In Progress]
Mixed Designs
According to Field (2017), mixed designs are used to compare several means when there are two or more independent variables. Further, at least one of the independent variables has been measured using the same participants and one has measured using different participants. In other words, there is one between-subjects factor and one within-subjects factor. Overall, mixed designs provide an analysis of the effects of each independent variable’s effects separately while also looking at their interactions.
Although mixed designs have increased power due to smaller error terms and allow generalizability, they also have the disadvantage of being complex. In other words, mixed designs require all assumptions for between- and within-subjects designs to be met. For example, mixed designs must meet the assumption of independence of errors (between-subjects) and sphericity (repeated measures).
In order to understand where the variance is located in mixed designs, it is best to put it in a table. First, total variability is split in two: between and repeated.
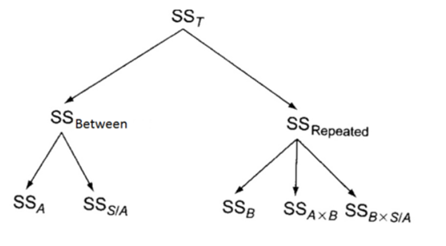
Next, when a simple mixed design is placed in a table, such as the one below, it becomes clearer where each term is found based on the row or column data.
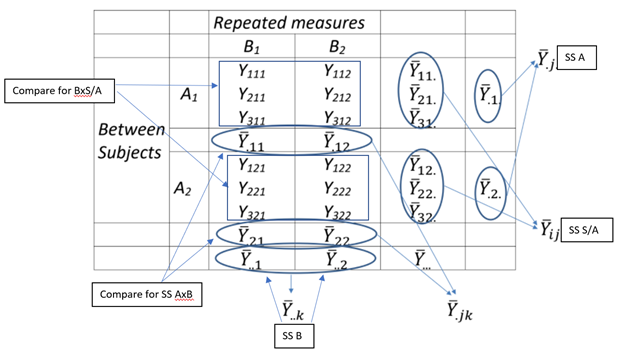
Additional information:
- An overview of between-subjects, within-subjects, and mixed designs: https://vault.hanover.edu/~altermattw/courses/220/readings/BetweenWithinMixed.pdf
- Mixed designs and SPSS instructions: https://www.discoveringstatistics.com/statistics-hell-p/porus-comparing-means/mixed-designs/
Bringing it All Together
After completing the directed studies course, Quantitative Methods of Ed Tech, I believe I have a better grasp of the foundational concepts of statistics. However, if I don’t use this knowledge and these skills that I have developed, I will again forget much of what I have learned. To prevent that, my plan is to continue to work with this blog and keep notes of sites and resources that were and are useful to me. To that end, one area that I believe I still need practice with is deciding what test to use.
Howell (2017) provides a very useful decision tree on the back cover of the Fundamental Statistics for the Behavioral Sciences textbook (a similar one can be found here: https://commons.wikimedia.org/wiki/File:InferentialStatisticalDecisionMakingTrees.pdf). Although I do not think I will ever be an expert at statistics, developing a better understanding of when and why different tests are appropriate is a useful skill for determining the quality of research studies and well within my capabilities. So, I will conclude my statistics posts by saying, I might be done this course, but my learning has only just begun.
Additional resources:
- A review of ANOVA tests, one-way to factorial: https://www.statisticshowto.com/probability-and-statistics/hypothesis-testing/anova/
- A free introductory statistics textbook and lab manual: https://www.crumplab.com/statistics/ and https://www.crumplab.com/statisticsLab/
- Free tutorials that cover basic statistics: https://stattrek.com/
References
Field, A. (2017). Discovering statistics using IBM SPSS statistics (5th ed.). SAGE Publications.
Howell, D. C. (2017). Fundamental Statistics for the Behavioral Sciences (9th ed.). Cengage Learning.